说明:本文阐述了ΔG既从热力学上决定反应自发性和平衡电位,又从动力学上通过影响中间体吸附能和活化能垒控制反应速率。本文还简要介绍了利用密度泛函理论(DFT)计算吸附自由能ΔGads的方法。
吉布斯自由能(Gibbs Free Energy,ΔG),作为经典热力学中判断过程自发性和平衡状态的核心状态函数,不仅从宏观上决定了反应能否发生及其进行的限度(平衡电位),更在微观层面通过决定反应中间体的吸附强度,深刻影响着反应路径的选择和活化能垒的高低(反应速率)。
因此,ΔG是连接电催化反应热力学基础与动力学表现的关键桥梁,是理解和设计高效电催化剂的核心描述符。
什么是吉布斯自由能(G)
吉布斯自由能(G)定义为:G=H-TS,其中H是焓,T是热力学温度,S是熵。对于在恒温恒压条件下发生的化学反应或过程,其吉布斯自由能变(ΔG)是判断过程自发性的终极判据:ΔG<0><!--0-->:过程自发进行;ΔG=0:系统处于平衡状态;ΔG>0:过程非自发进行,其逆过程自发。
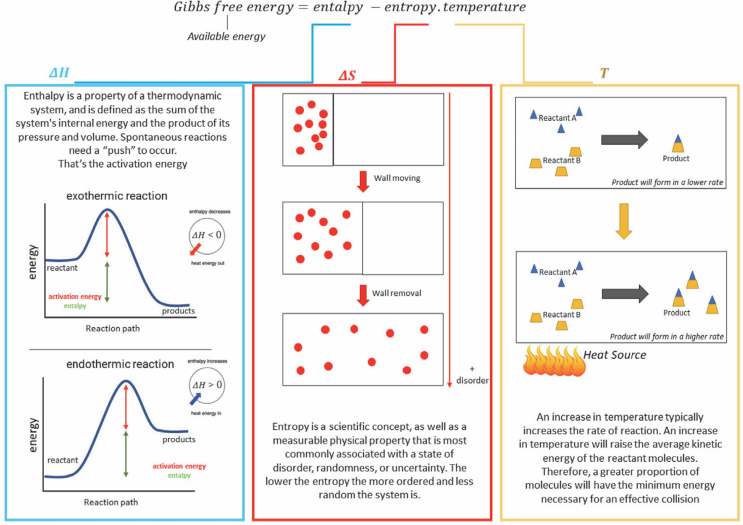
图1 吉布斯自由能方程释义。DOI:10.5772/intechopen.98766
在电催化中,反应通常发生在电极/电解质界面,涉及电子的转移(电荷转移步骤)和化学键的断裂与形成(化学步骤)。ΔG综合了系统的能量变化(焓变ΔH)和有序度变化(熵变ΔS),精确刻画了在特定温度、压力和组成条件下,反应驱动力的大小。


吉布斯自由能中的热力学
对于一个通用的电催化还原反应:Ox+ne-→Red。其标准吉布斯自由能变(ΔG⁰)与该反应的标准平衡电极电位(E⁰)通过能斯特方程的核心关系式紧密相连:ΔG⁰=-nFE⁰。
其中:n是反应转移的电子数;F是法拉第常数(96485C/mol);E⁰是标准电极电位(相对于标准氢电极,SHE)。
该公式决定了反应倾向:ΔG⁰<0><!--0-->意味着E⁰>0,表明还原反应相对于SHE是热力学自发的;反之亦然。此外,知道ΔG⁰即可计算出理论上的可逆电位E⁰,这是评估任何电催化反应所需最低驱动力的基准。
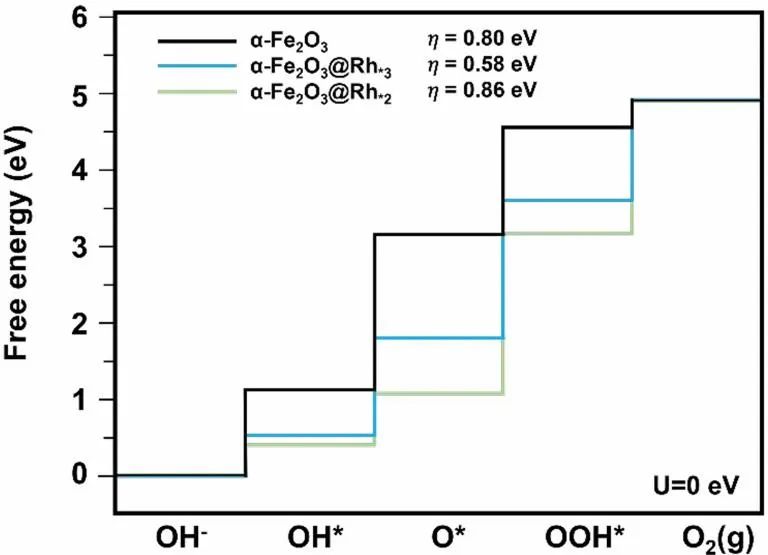
图2 α-Fe2O3@Rh*3和α-Fe2O3@Rh*2的自由能和计算过电位。DOI:10.1021/acsami.3c04458
对于非标准态,能斯特方程给出了电极电位E与实际反应物/产物活度(或浓度)的关系:E=E⁰-(RT)/(nF)*ln(Q),其中Q是反应商。
反应的ΔG则可表示为:ΔG=-nFE=ΔG⁰+RTln(Q)该式清晰地表明,施加的电极电位E直接调控着反应的驱动力ΔG。
电催化正是通过施加过电位(η=|E-Eeq|),使ΔG足够负(对于还原反应)或足够正(对于氧化反应),从而驱动反应以可观速率进行。
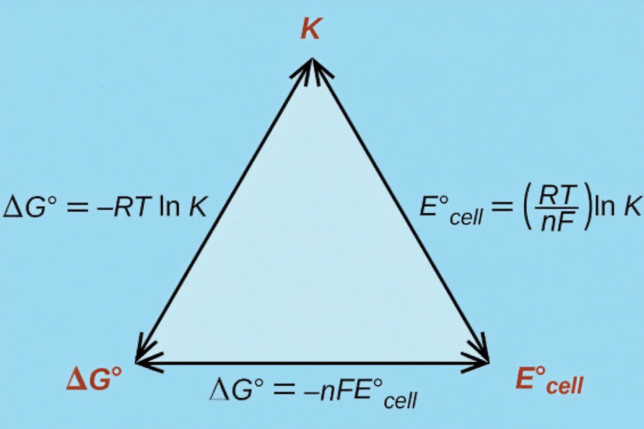
图3 E、G和Q之间的关系图。DOI:10.35537/10915/99291


动力学
热力学决定了反应能否发生(ΔG<0><!--0-->),而实际反应速率则由动力学控制,核心是活化吉布斯自由能(ΔG‡)。
根据过渡态理论,反应速率常数(k)与ΔG‡的关系为:k=(kBT/h)*exp(-ΔG‡/RT)。其中kB是玻尔兹曼常数,h是普朗克常数。
在电催化中,反应速率(通常表示为电流密度j)强烈依赖于施加的过电位η。描述这种依赖关系的核心模型是Butler-Volmer方程及其在特定情况下的近似形式(如Tafel方程)。
Butler-Volmer方程揭示了电流密度与过电位η和活化能(与ΔG‡相关)的指数关系:![]()
。其中:j₀是交换电流密度,是反应本征活性的度量,直接与活化能垒ΔG‡相关,
![]()
。α是传递系数(通常≈0.5),描述电极电位如何分配以降低正向或逆向反应的活化能垒。
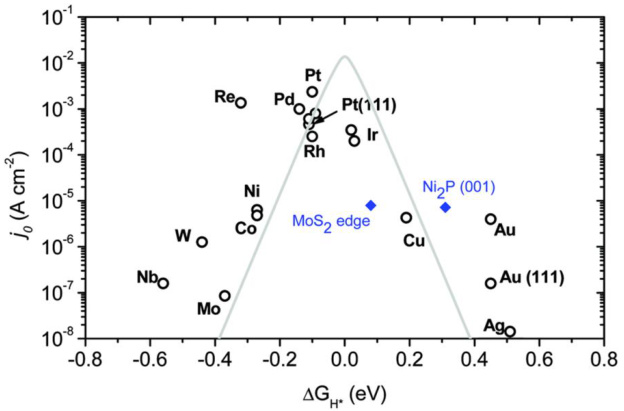
图4 火山图(实验测量的交换电流密度j0作为理论H化学吸附自由能ΔGH*的函数)用于HER。DOI:10.32657/10356/73265
电极电位E(或过电位η)通过改变反应坐标上各态(尤其是过渡态和中间态)的吉布斯自由能,从而改变活化吉布斯自由能ΔG‡,最终决定反应速率j。催化剂的本质作用就是降低关键步骤(通常是速率控制步骤)的ΔG‡,从而在较低的过电位下获得较高的反应速率(高j₀)。
如图5,电势升高时,过渡态TS2的能量显著降低(如从+1.8eV降至+0.3eV),表明电极电位可选择性降低特定步骤的ΔG‡。速率控制步骤(Rate-DeterminingStep,RDS)随电位变化:低电位时TS1为RDS(能垒最高),高电位时TS3成为新RDS。
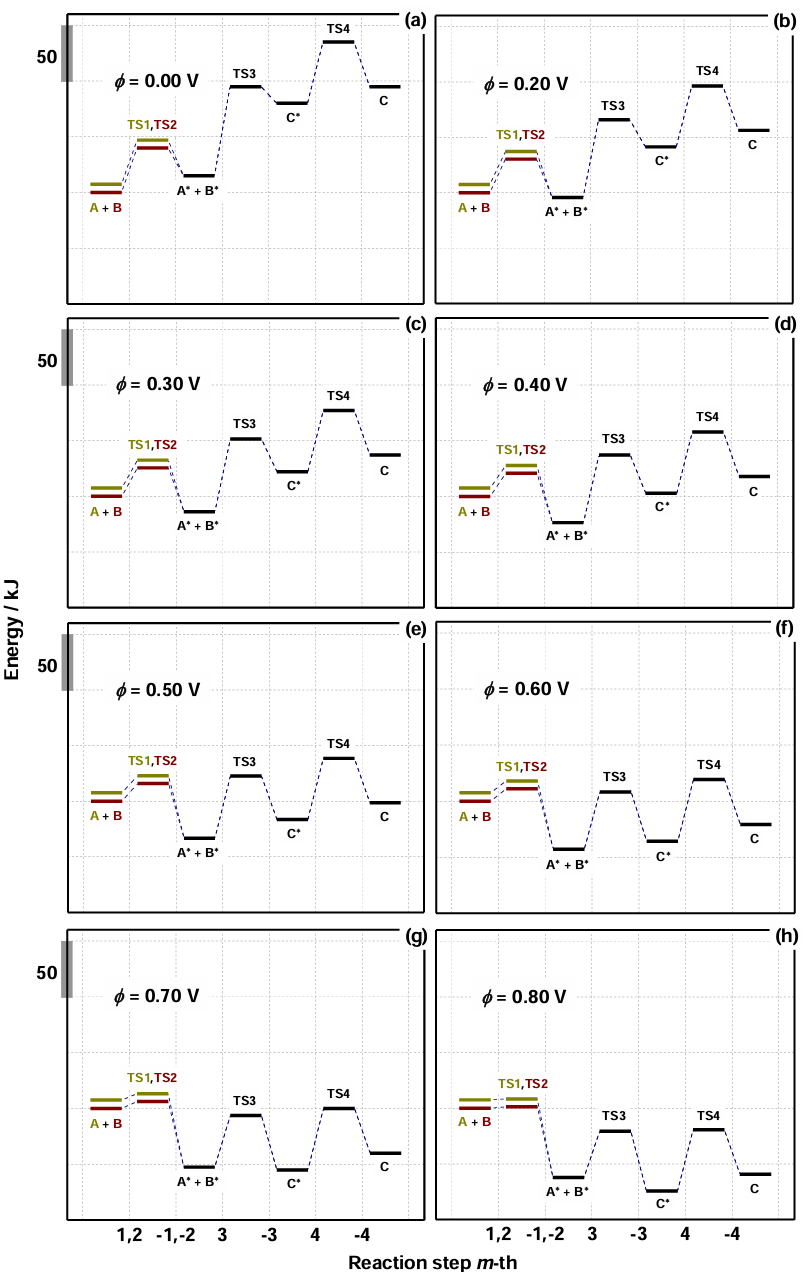
图5 电化学过程的反应物(A和B)、中间体(A∗、B∗和C∗)、产物(C)和过渡态(TS1、TS2、TS3和TS4)之间在不同电位φ的相对能量图。DOI:10.1021/acscatal.0c02359


吉布斯自由能的计算与模拟
理论计算,特别是基于量子力学的密度泛函理论(DFT),已成为计算电催化反应中吉布斯自由能变(尤其是吸附自由能ΔGads)的核心工具,为理解机理、预测活性和设计催化剂提供了强大支持。
基本计算流程
结构建模:构建催化剂表面模型(如金属板、金属氧化物表面、团簇、单原子位点载体等)。
几何优化:使用DFT计算优化催化剂表面、反应物、产物、中间体以及它们吸附在表面上的复合结构的几何构型,找到能量最低的稳定结构。表面模型需考虑真空层(≥20Å)以防止周期性干扰,并使用超晶格模拟实际界面
能量计算:计算优化后各结构的电子总能(EDFT)。
零点能校正:计算各物种的振动频率,得到零点振动能(ZPE)。EZP(corrected)=EDFT+ZPE。
焓变(H)与熵变(S)计算:在理想气体/谐振子近似下,利用频率计算得到焓变(ΔH)和熵变(ΔS)的校正项(通常在298.15K)。
ΔH=ΔEDFT+ΔZPE+ΔHtrans+ΔHrot+ΔHvib(对气相分子)
ΔS=ΔStrans+ΔSrot+ΔSvib(对气相分子)
吸附态:吸附物种的熵变计算较为复杂,通常采用近似,如忽略吸附分子的平动和转动熵,只考虑振动熵;或参考类似体系的经验值。这是计算ΔGads的主要误差来源之一。
吉布斯自由能计算:ΔG=ΔH-TΔS。
考虑溶剂和电场
溶剂化效应:水溶液环境对反应自由能影响巨大。常用方法包括隐式溶剂模型(如PCM,VASPsol)、显式溶剂分子模型(在吸附层加入水分子)或混合方法。这是当前计算的重要挑战和热点。
催化剂表面的简单模拟模型及其与实际情况的相关性如图6所示,其中以HER(氢氧燃料电池)为例。在计算代码中,黑色方框中的单元格会沿三个方向周期性重复,以建立长固体表面。最上面的一层用深色突出显示,这是反应发生和中间体生成的地方。
反应中间体的吸附性质,作为决定催化剂活性的关键因素,在模拟催化表面上进行计算。在实验条件下,电极(作为反应催化剂)被水环境包围;而在模拟中,我们使用真空来表示这个空间。在大多数情况下,这种近似不会影响催化趋势;然而,在CO2ER领域,一些中间体对水敏感,溶剂化效应不能忽略不计。
对于这些情况,通过利用先前的理论发现,将水溶液对这些中间体结合能力的定量影响添加到总电子能量中。
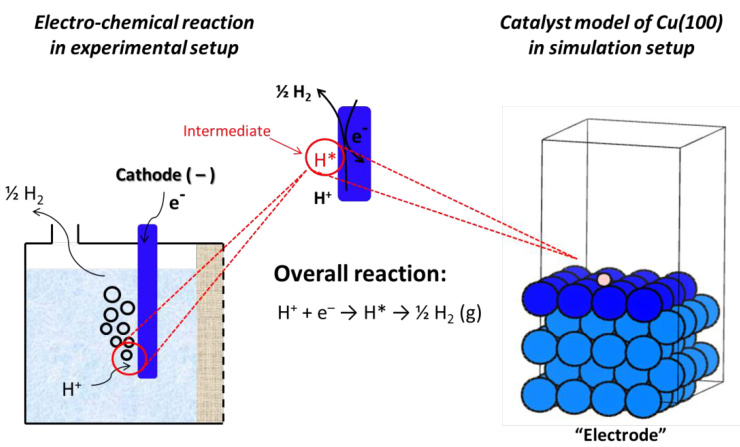
图6 实验情况与模拟模型示意图DOI:10.32657/10356/73265
电极电位效应:DFT计算通常在电荷中性条件下进行。施加的电极电位改变了电极表面的电子化学势(费米能级)。通常的处理方法是:将电子e⁻的化学势(μe)与电极电位E关联:μe=-eE-常数(相对于某个参考,如SHE)。
对于反应A+e⁻→B,其自由能变ΔG=GB-GA-μe。通过调节计算体系的电荷状态(添加/移除电子)并考虑其能量变化,可以模拟不同电位下的ΔG。恒电位计算方法是当前前沿。
关键中间体吸附自由能(ΔGads)计算
ΔGads是电催化计算中最核心的量之一。以*+X→X*为例:ΔGads(X*)=G(X*)-G(*)-G(X)。其中G(X*)为吸附态X*的总吉布斯自由能;G(*)为干净催化剂表面的吉布斯自由能。G(X)为自由分子X在气相(或溶液相)中的吉布斯自由能。计算时需要特别注意X的参考态(气相/溶解态/标准状态)以及如何准确计算G(X*)(特别是熵的贡献)。
计算的优势与局限性
优势:提供原子级理解,揭示反应机理和速率控制步骤。预测中间体吸附强度(ΔGads),构建火山图,筛选潜在催化剂。指导实验设计(如预测合金、掺杂、应变效应)。研究难以通过实验表征的界面过程和短寿命中间体。
局限性/挑战:
DFT泛函的选择(如对强关联体系)、色散力校正、溶剂化模型精度、熵处理的近似性都会带来误差(通常认为ΔG误差在0.1-0.3eV)。表面模型可能无法完全反映真实催化剂的复杂性(缺陷、边角位点、动态重构、覆盖度效应、电解质离子影响)。
精确描述固液界面结构和溶剂化效应极其困难。精确模拟实际工作电位下的电荷状态和电场分布仍是挑战。直接计算反应能垒(ΔG‡)通常比计算ΔG更耗时且不确定性更大。


总结
吉布斯自由能(ΔG)是理解与优化电催化过程的核心物理量。它连接了反应的热力学驱动力(电位调控)与动力学速率(活化能垒),是评估催化剂性能的关键描述符。基于DFT的ΔG计算为揭示反应机制和理性设计高效电催化剂提供了强大但仍有挑战的工具。